Сегодня я собираюсь показать некоторые «конструктивные подробности» «линеаризации-экваторизации» («проецирования на линию Экватора») Знаков Западного Зодиака.
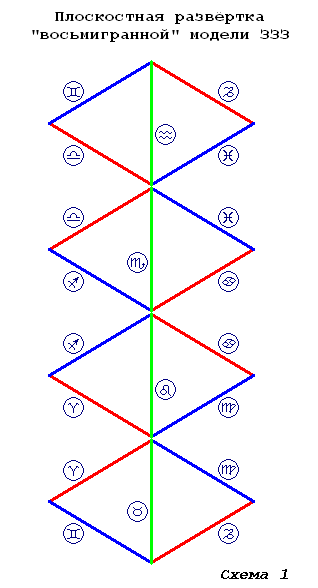
Для начала посмотрим, какова «плоскостная развёртка» «восьмигранной» и «сферической» моделей ЗЗ (см. Схему 1 и Схему 3 в «Проекциях» Западного Зодиака на Октаэдр и Сферу). «Октаэдр» ЗЗ на плоскости разворачивается примерно так:
А «сферическая» модель – примерно так:
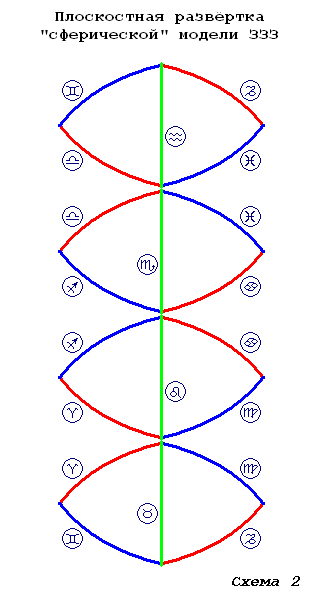
Самое главное, что мне хотелось на этих схемах показать (и что, как я надеюсь, с лёгкостью различит всякий любознательный Читатель), так это буквальные «смысловые и фактические» аналоги «стихийных» квадрантов ЗЗ (в схемах материала Становление как ПервоПринцип и «школьная геометрия») как они есть в виде равносторонних треугольников в «октаэдрической» и «сферической» «поверхностных» моделях ЗЗЗ (причём в «сферической» модели треугольники не просто равносторонние, но вдобавок ещё и прямоугольные).
Значение Русского «Дитя» в Эпоху Водолея
О том, что Становление в качестве Третьего Начала обще-диалектической Триады «закономерно гарантирует» равноправное и гармоничное СамоВзаимоОпределение Первых Двух Начал и что в Общинно-Родовой Триаде Оно соответствует «Дитю», я прежде уже сообщал. Сейчас же я скажу «нечто существенное и принципиально новое» о Третьем Начале применительно к «разоблачаемым сокровищам» астрологической традиции Запада.
Напомню, что «любой точке» «пространства» Становления (окружности) в «школьной геометрии» соответствует вполне конкретная «пара точек» в «пространствах» Одного и Иного. Зная «положение» «точки» Становления, мы просто и «чисто практически геометрически» «опускаем» перпендикуляры на «оси» Одного и Иного:
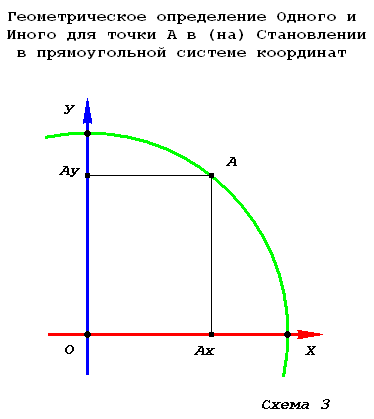
Зная «положение» «точки» А только в «пространстве» Одного или только в «пространстве» Иного в прямоугольной системе координат, мы также легко определим и «положения» «недостающих» двух членов обще-диалектической Триады в любом квадранте «чисто практически геометрически», восстановив соответствующие перпендикуляры.
А вот для «чисто математического» решения последней задачи придётся уже использовать как минимум «квадратные» уравнения.
Перехожу к «реальности» поверхностей Октаэдра и Сферы.
На Схеме 4 показано несколько вариантов «прописки» Трёх обще-диалектических ПервоПринципов в грань Октаэдра в терминологии Триады Общинно-Родовой, в «цветах» предыдущей схемы и в «видимостях» «равносторонней» и «равнобедренно-прямоугольной»:
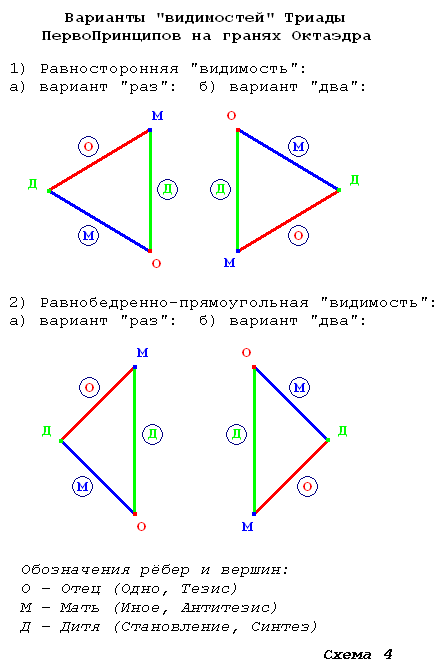
Схема 4 мне понадобилась для того, чтобы как-то помягче-подоходчивей показать как, каким образом «работает» Становление в качестве «законодателя» и «определителя» для Одного и Иного «по аналогии» со Схемой 3 в «реальностях» поверхности Восьмигранника и Сферы.
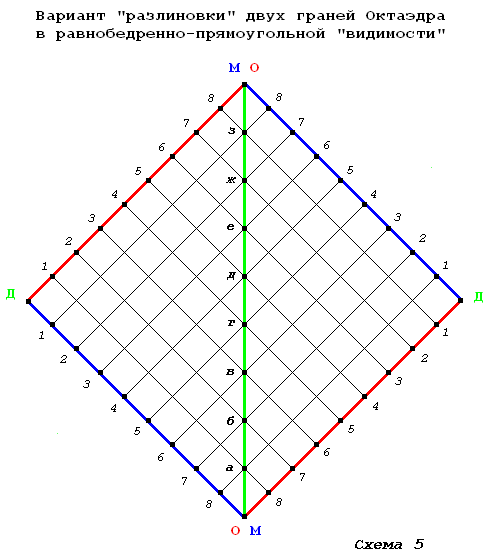
На Схеме 5 я даю вариант «разлиновки» одного из ромбов Схемы 1 с обозначением вершин как на Схеме 4 и в равнобедренно-прямоугольной «видимости»:
А на Схеме 6 то же самое, что и на Схеме 5, но в «видимости» равносторонней:
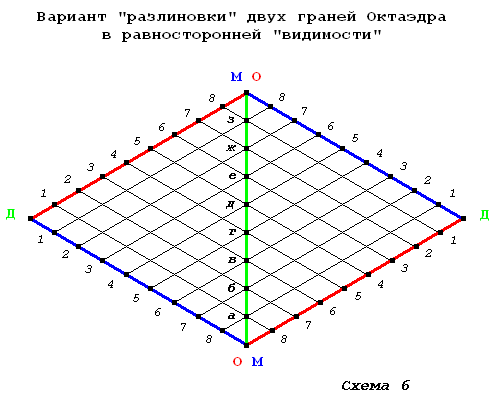
Что я хотел подчеркнуть последними двумя схемами? Тот «факт», что если в «школьной геометрии» допустимо «опускать перпендикуляры», то на поверхности Октаэдра для «демонстрации» «законодательной силы» Становления необходимо «строить параллели» к соответствующим рёбрам.
Это, конечно, важная «конструктивная» подробность, но не единственная эйдетическая (смысловая) и тем более – не главная. В отличие от «школьной геометрии», на поверхности Восьмигранника в каждой его грани «пространства» Трёх ПервоНачал Диалектики не «просто абстрактно» «равноположены», но и зримо «величинно» равны, что, в свою очередь, приводит нас к весьма существенным выводам.
Прежде чем «озвучивать» эти выводы, несколько слов о поверхности Сферы. Всё, сказанное об Октаэдре, по сравнению со «школьной геометрией», относится к ней в полной мере. Имеются, однако, некоторые чисто «терминологические» и «технические» особенности. Говоря о поверхности Сферы, мы пользуемся, к примеру, понятиями «октант» (вместо «грани») или «четверть Большой Окружности» (вместо «ребра»). «Параллели» же на поверхности Сферы в каждом октанте строятся не линейкой (как на гранях Октаэдра), а циркулем из соответствующих вершин соответствующего октанта.
И вот теперь о самих этих «весьма существенных выводах». Самое неожиданное и поразительное, на мой взгляд, заключается в том, что в «восьмигранной» и «сферической» моделях ЗЗ положение любой точки в «детском месте» (в «пространстве» Становления) не просто имеет свои «родительские проекции» («это» само по себе наличествует и в «школьной геометрии»), но имеет именно такие «родительские проекции» (строго определённые соответствующие значения в «пространствах» Одного и Иного), которые при обыкновенном «арифметическом» сложении в точности равны «целому» Дитю данной конкретной грани или данного конкретного октанта.
Для меня «это» - настоящее Чудо! В реальной геометрии (на поверхности Сферы) «взаимоотношения» между «членами» Обще-диалектической Триады ПервоНачал «регулируются» самой простой и элементарной математикой, или арифметикой.
[Я вполне осознаю, что «здесь и сейчас» произвожу «развёртывание» «детского места» по «типу-закону-алгоритму Отца», с точки зрения канонов православной христианской догматики и апофатики. «Строгие модификации» разворачивания по типам «детскому» и «материнскому» я прекрасно себе представляю, но пока надеюсь обойтись без «избыточных сложностей».]
А пока… Ухожу в «паузу»…
Лео Шарк
Первоисточник => Солнечное Искусство
